ケース面接に必ずと言っていいほど出題されるフェルミ推定。今回はそんなフェルミ推定の基礎的な厳選問題集を解説付きでご紹介します!
本記事で紹介する解説はあくまで一例です。フェルミ推定やケース問題は正解はありません。なので受験勉強のように答えを求めてそれを覚える、という学習方法は適しません。基本的には自分の頭で考えるということが非常に重要となります。
本記事では一定の思考の型を解説しているので、書いてあることをもとに自分なりの仮説や論理を付け加えて、自分なりの回答を作るように心がけましょう。
また、今回はケース面接で出題されるフェルミ推定の解説付き問題集でしたが、他にもケース面接で出題されるビジネスケース、パブリックケースについての解説付き問題集もあるのでぜひあわせてご覧下さい!
【MBB内定者の解説付き】 戦略コンサルの面接で出題されるケース面接の厳選問題集〜基礎編〜【図解での解説付き】ケース面接の厳選問題集〜パブリック編〜
それでは早速始めましょう!
目次
フェルミ推定の問題の種類
本記事では以下の4つの系統を1問ずつ扱います。系統ごとに式分解の方法やセグメンテーションなどは共通する部分が多いので、それぞれ1問ずつこなすことでかなり基礎を固めることができます。

この系統には当てはまらない問題も少なくはありますが存在します。そのような問題についてはReverseがご提供している、ケース対策サービスで主に取り扱っております。
【フェルミ推定の厳選問題集】問題1:売り上げ推定系(マクロ)
売り上げ推定系の中でもマクロ系は、いわゆる市場規模系を求める問題系統です。
お題は
『自動車販売の市場規模を求めよ』
です。思考時間は5分で解いてみて下さい。
それでは早速解説していきます。
前提確認
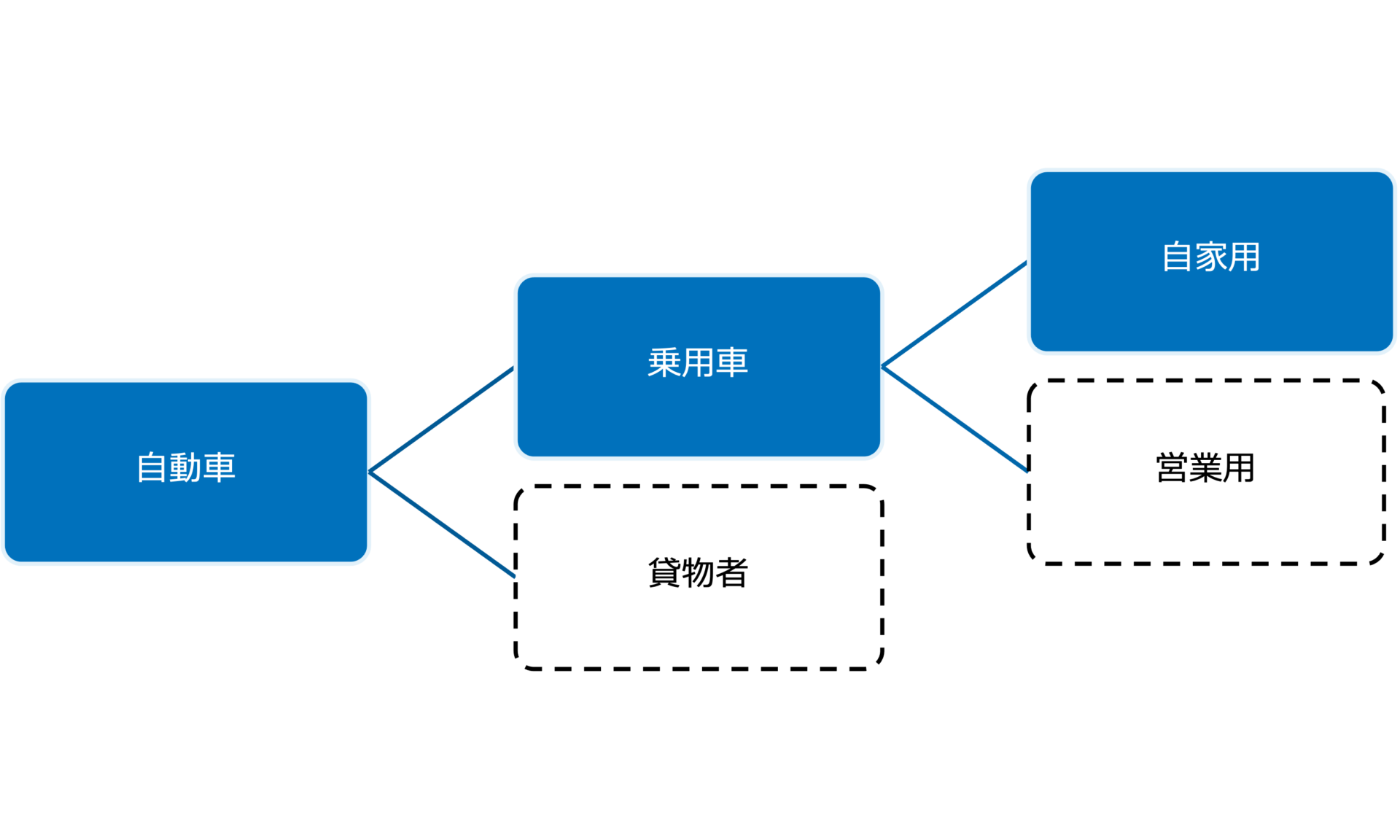
このお題については、地域、年度と自動車販売の定義を定める必要性があります。地域、年度については2021年の国内での市場規模と設定します。また自動車販売の定義ですが、レンタルサービスなどは含めずに、新車・中古車を完全に所有権を渡すような売り切りのもののみを推定することとします。また車種については、貨物車は含めずに乗用車のみをスコープとします。
そして立式に入る前にさらに乗用車についても保有主体が個人の自家用車と、法人の営業用車の2つがあることに気をつけなければいけません。個人と法人の、主体の数(世帯数と法人数)と保有割合、台数を鑑みると、個人の自家用車の方が桁が変わる程度に大きそうなので、今回は乗用車の中でもさらに自家用車のみを推定します。
立式
立式は以下のようになります。

この式は現在存在している自家用車のうち、買い替えが発生する分の市場規模を求めています。
初めてこの問題に取り組む方の多くは、新たに購入する世帯については別式で立てて求める方がいらっしゃいます。その点については後ほど補足として付け足すので是非お読みください。
セグメンテーション・数値代入
セグメンテーション・数値代入は以下のようになります。

今回のセグメンテーションの切り口は、地方と都市部で分けました。このセグメンテーションにした理由は大きくファクターの値が変わりそうだからですが、その背景にある仮説としては、
- 都市部の方が電車のインフラが発達しているのと地価が高いため車の保有率が大幅に下がりそうな一方で、地方の方はほぼ移動手段が自家用車のため保有率が非常に高い
- 逆に都市部で自家用車を保有するような家庭は高所得である確率が高そうなため、車の単価も上がりそう
があります。
これらを計算した結果、年間の自家用車の販売台数が250万台、市場規模が10.3兆円となりました。
ちなみに2021年の新車販売台数が444万台となっています。今回考えたのが自家用車のみで、オーダーとしてはあっており、その他も合わせるとかなり近い数値になると思われるので、精度の高い推定と言えると思います。
立式についての補足
先ほど、式分解の際に買い替えのみの式分解で十分と述べましたが、その背景にある前提として、自家用車の数は一定という前提を置いています。
より分かりやすいようにストックとフローの概念を使って説明します。ストックというのは現在存在している数、インフローはストックに新たに足される数、アウトフローはストックから外される数です。例えば年単位でストックの変動を考えようと思ったら
来年度のストック量=今年度のストック量+(インフロー ー アウトフロー)
となります。
これを今回の問題に当てはめると、ストックが自家用車の存在台数、初めて購入する世帯の自家用車の台数がインフロー、車を保有しなくなる世帯分の台数がアウトフローとなります。
このインフローとアウトフローが等しく、ストックが一定という仮定を置くことにより、ストックの一定割合が買い替えるという式のみで市場規模を求めることができます。

仮にその過程を置かない場合は、初めて購入する世帯分の式と、現在保有している世帯のうち買い替えを行う割合を入れた式の二つが必要になり時間がかかります。そのため、今回はこのストック一定の仮定をおきました。
ここの議論は初心者の方には少し難しいと思いますが、ある程度慣れてくると必ず疑問を持つところですので、一度流し読みで何となく理解しておくだけでも大丈夫です。またご自身で疑問を持った際に読み返してみて下さい。
【フェルミ推定の厳選問題集】問題2:売り上げ推定系(ミクロ)
売り上げ推定系の中でもミクロ系は、いわゆる1店舗の売上などの、規模が小さい売上を推定するものです。同じ売上推定系でも、マクロとは式分解の筋の良さなどは大きく異なるので、その辺をポイントに考えてみて下さい。
お題は
『渋谷にあるカラオケBOX1店舗の平日1日の売上額』
です。
この問題も同様に5分間自分で測って考えてから下の解説をご覧下さい。
前提確認
特に考えておくべき不確定事項としては、いつの時期か?どのような店舗か?と言ったものが挙げられますので、以下のように前提を定めました。
- コロナの影響は加味しないものとする。
- 営業時間は24時間とし、カラオケ店の中でも比較的低価格帯の店舗とする。
立式
式分解の切り口としては大きく、需要側・供給側の二つが挙げられます。
需要側は例えば
1日で渋谷に来る人数×遊びに来ている割合×カラオケ利用率×クライアント選択率×客単価
が考えられますが、『1日で渋谷に来る人数』が特に推定のロジックが立てづらく、筋があまり良さそうにありません。
一方で供給側の式分解は
フロア数×1フロアあたりの部屋数×1部屋の平均収容可能人数×稼働率×
1時間あたりの回転数×営業時間×客単価
が考えられます。これだと先ほどの『1日に渋谷に来る人数』ほどボラティリティが大きそうなファクターがありません。そのため、今回は供給側からの式分解を用います。
ちなみにこの供給側からの式分解を抽象化すると
『キャパシティ×稼働率×回転数×営業日数』
の式分解モデルです。
このように、ミクロ系ではマクロ系と逆で、供給側からの式分解の方が求めやすいのが特徴です。
セグメンテーション
セグメンテーションは
『時間帯によって客層や人数、また提供商品の値段も大きく変わる』
という仮説をもとに、時間帯で切りました。
何個のセグメントに切るかについては、おおよその差が出そうな中で、時間内に求められそうな数という意味では3〜4つ程度のセグメントに切るのがおすすめです。
数値代入
セグメントごとのファクターの値は以下のようになります。

前三つのファクター(フロア数〜1部屋の平均収容可能人数)はセグメントごとによらず固定されています。
それ以降のファクターについては
- 稼働率は、平日の午前が最も少なく、午後から学生や主婦層、夜間は社会人も加わり増加する
- 回転数は滞在時間の平均が2時間、深夜は帰宅が難しいので時間が伸び、一方午前は回転が早い
- 客単価は6〜18時は400円/1時間、それ以外は需要の増加に伴い値上げして600円/1時間
としました。
これらを計算すると約120万円となります。1店舗の売り上げとしてはやや大きい気がしますが、カラオケBOXの中でも渋谷は非常に規模の大きい店舗であるため、ある程度妥当性があると思われます。
【フェルミ推定の厳選問題集】問題3:個数推定系(所有物系)
お題は
『日本に存在する猫の数』
です。少し取り掛かりにくい問題ですが、そこが本問題のポイントとなります。
これも制限時間5分で考えてみて下さい。
前提確認
今回重要なのが、この前提確認の部分です。
日本に存在する猫を構造的に分けると以下のようになります。
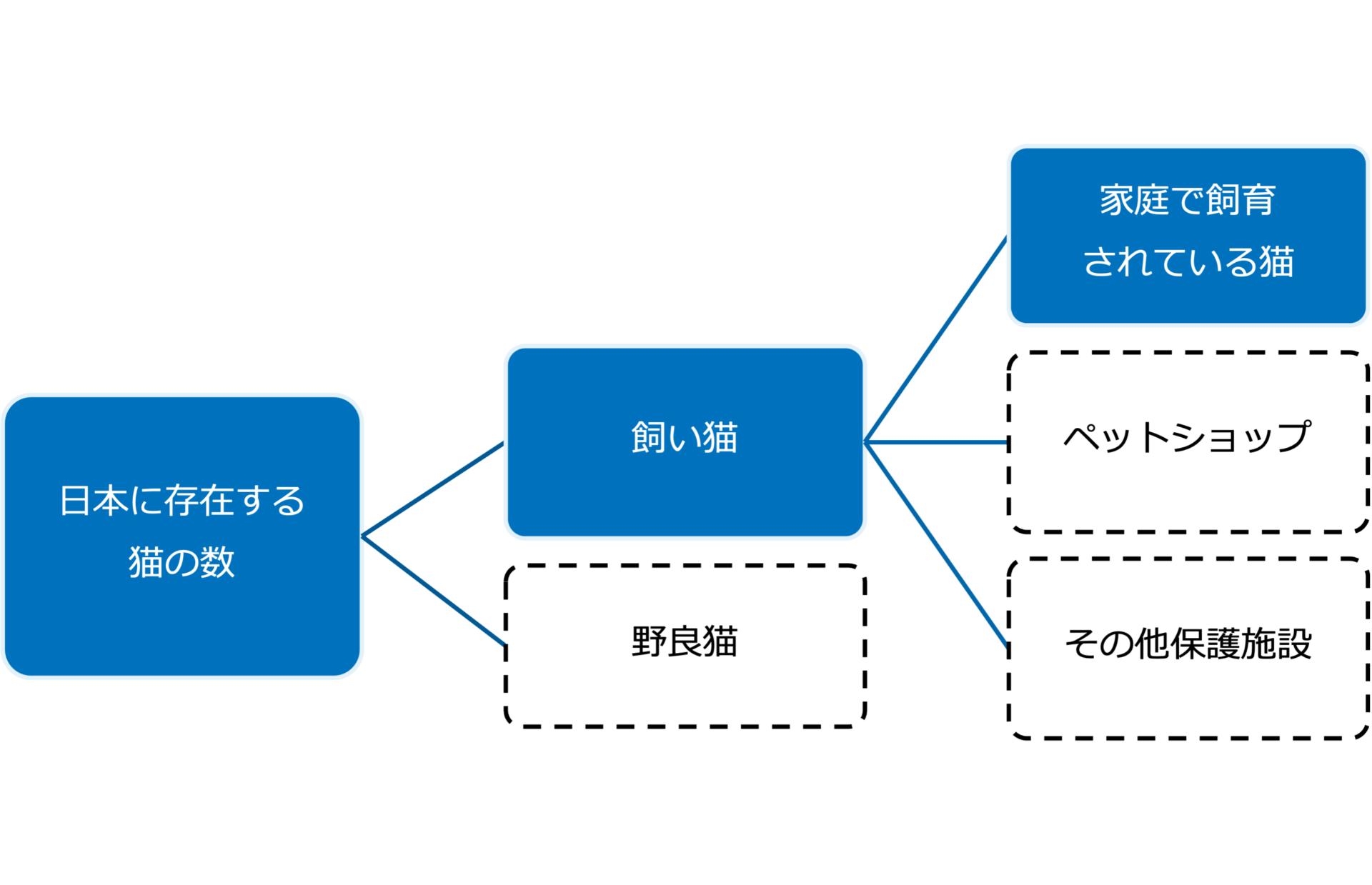
これら全てを式分解して推定していると、時間内に終わらない可能性が高いです。その為『日本に存在する猫の数』の中で占める割合がかなり高いであろう『家庭で飼育されている猫の数』を今回は推定することとします。もし制限時間内に他の項目についても考える余裕がありそうならば、式分解だけでも考えてみると良いでしょう。
今回はセグメンテーションを完全に行わずに、各ファクターの値を加重平均を用いて部分的なセグメンテーションを行います。こうすることで短い思考時間の中でも、ある程度論理と仮説を持ったアウトプットを作ることができます。
立式・数値代入
式分解と最終的な数値代入は以下のようになります。

所有物系だとこのように所有している主体目線で式分解していくことが多いです。
この式分解でポイントは、『ペット飼育可能割合』と『ペット飼育率』を分けたことです。ペット飼育するかどうかには『金銭的な余裕』や『面倒を見ることができるか』などの制約もありますが、『マンションの規則』のような物理的に飼育することができないという制約が大きくあります。その、『物理的に飼育することができない』という要素を別ファクターで分けることで飼育の制約についてMECEに考えることができます。
各ファクターについては以下のように考えました。
- 世帯数
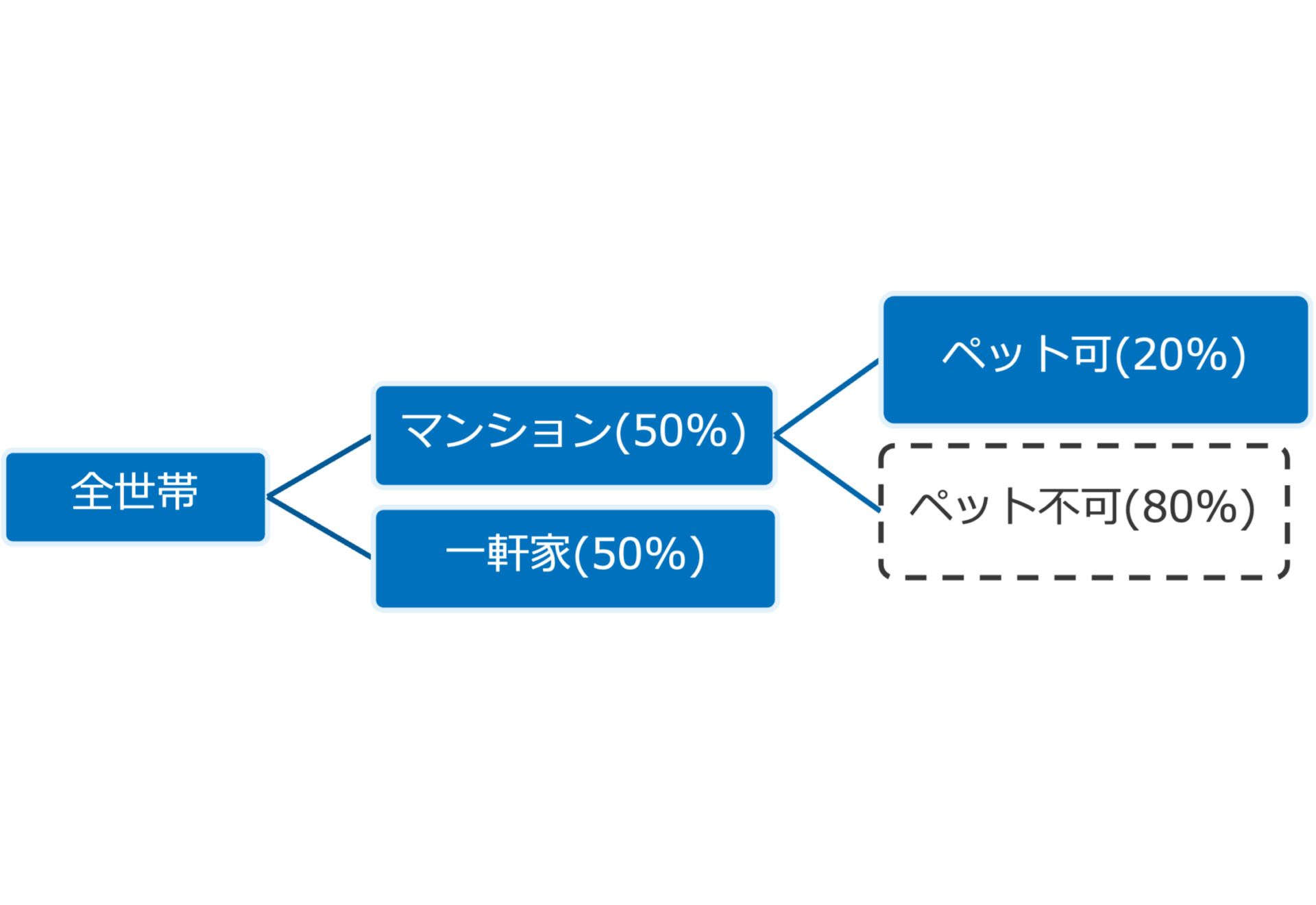
人口(1.2億人)÷1世帯の平均人数(2.5人) - ペット飼育可能割合
先にも説明したように、規則的に飼育可能な割合を指すことにしました。
主な理由はマンションの規則と考えた為、図のように世帯をセグメント分けし加重平均で考えました。
- ペット飼育率
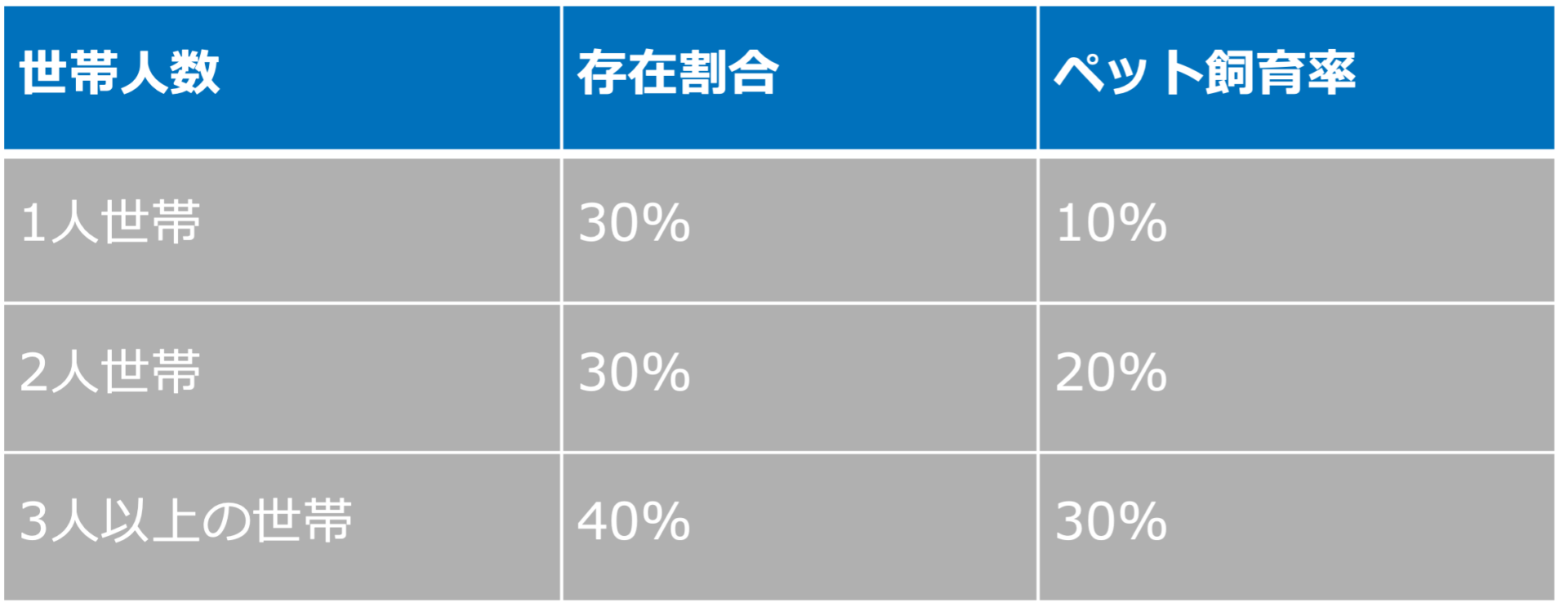
飼育率は、
『世帯年収が高い方が高い』
『人数が多い方がペットの面倒を見れる為高い』
『子供がいるような家庭の方が高い』
という仮説のもと、図のように世帯人数でセグメント分けして加重平均を取りました。
- 猫選択率
猫:犬:その他=1:1:1と考えて30%に設定しました。 - 平均飼育数
10件に1件は2匹を飼育と仮定して加重平均で1.1匹としました。3匹以上飼っている世帯は存在するとは思いますが、インパクトとしては小さいと考え省略しました。
これらを掛け合わせると約300万匹となります。一般社団法人ペットフード協会の公開データによりますと、2020年の猫の飼育総数は964万頭とのことです。少し推定値よりは大きいですが、桁は合っており合格ラインと言えます。
【フェルミ推定の厳選問題集】問題4:個数推定系(非所有物系)
最後の問題の種類は個数推定系の中でも、非所有物系です。日本に存在する個数とか、そういった類の問題です。
そこで最終問題は
『日本に存在する歯科医院の数』
です。これも時間は5分で考えてみましょう。もし余裕のある方は思考時間2分でも回答を作ってみましょう。
この問題についてはいくつか考え方がありますので、それも合わせて解説していこうと思います。
前提確認
この問題については、いつ頃かというスコープのみで良さそうなので、2021年として考えてみます。
立式・数値代入
この問題については何個か筋の良さそうな式分解があります。
一つは非所有物系で使われることの多い、所謂『面積ベースの立式』と言われるものです。
『面積ベースの立式』とは、求めたい物体1つが、平均どれくらいの面積間隔に存在するか予測を立て、日本の面積をその予測を立てた面積で割るというものです。
もう一つの立式は『需要÷供給』です。
この立式は、こういう歯科医院の数のような、サービス提供者と供給側の需給のバランスが取れており、需要と1主体の供給量が推定しやすい場合に使われます。
今回だとこの二つの切り口、どちらも使えるのですが、面積ベースだと求めたい物体一つが平均どれくらいの面積間隔にあるかの仮説が少し粗くなり、推定値のボラティリティが大きくなりそうなことから、後半の『需要÷供給』の切り口で考えます。
『需要÷供給』を今回の問題に当てはめてみると、日本の歯科医院での年間総需要を、歯科医院1店舗での年間供給量で割ってあげると、日本に存在する歯科医院の数が出せます。より具体的に言うと
日本の歯科医院での年間総需要が、『年間歯科医院診察回数』
歯科医院1店舗での年間供給量が『歯科医院1店舗での年間診察回数』となります。

そしてそれぞれをより細かく立式し数値代入すると以下のようになります。

『年間歯科医院診察回数』については、結論3.6億回となりました。
数値代入に関しては
- 一人あたりの年間診察回数については、高齢者や歯が悪い人などの診察回数が多い人で2ヶ月に一回程度、その他のほとんど行かないような人は年に1回程度と考え、加重平均をとって3回
と考えました。

また『歯科医院1店舗での年間診察回数』については4800回となりました。
この式分解は問題2でやった、『キャパシティ×稼働率×回転数×営業日数』の式分解モデルです。
数値代入に関しては、
- 1日の回転数は、1時間あたり2回転の営業時間が8時間程度
- 年間営業日数については、平日のみの開業と考えて250日
と設定しました。
どちらも加重平均で数値代入しましたが、時間に余裕のある場合はセグメンテーションまで行ってみましょう。
これらの結果から、
日本の歯科医院の数
=年間歯科医院診察回数÷歯科医院1店舗での年間診察回数
=3.6億÷4800
=75,000
となります。
実際に厚生労働省による医療施設調査によると、2019年10月1日時点での歯科医院の店舗数は68,500店舗となっていました。かなり精度高く推定できた結果になっていますね。
終わりに
フェルミ推定の基礎問題集はいかがでしたでしょうか?
これら4つが頭に入っていれば今後の問題も考えやすくなると思います。一方でより複雑な問題や、ビジネスケースなどの問題についてはより対策が必要となってきます。
Reverseでは、マンツーマンで行うケース対策サービスをご提供しております。
ケース面接対策を通してトップティアの戦略コンサルティングファーム入社を目指すのは勿論、その後の経営層への基礎思考力育成を目指しております。
期間限定で、
米系トップティア戦略ファームメンターによる初回カウンセリングが無料
でお試しいただけるので、気になる方はポップアップのボタン、または公式LINEよりお問い合わせください
また、現在公式LINE追加してくれた方全員に『解説ポイント付きケース問題集』を配布しております。もちろん公式LINE追加は無料ですので、ぜひご登録下さい。



